Como Hacer Juegos: Las Matemáticas Que Todo Programador Debe Conocer.

En esta entrada de hoy, vamos a repasar las matemáticas básicas que como programadores de videojuegos en 2D tendríamos que conocer. Este será el primero de una serie de entradas que iré escribiendo de vez en cuando para agrupar y explicas las funciones matemáticas y físicas que se van usando a lo largo de los proyectos que iremos realizando. Además crearemos las clases complementarias que añadan funcionalidad útil a SFML 2.0 si fuera necesario.

Como situar una mosca en la pared: Espacio Euclídeo

El Problema es como situamos un objeto en el espacio de forma que podamos manipularlo matemáticamente, es decir de forma que el ordenador pueda entenderlo y posteriormente mostrarlo por pantalla.

La solución es establecer una serie de reglas, como especificar un origen desde el que empezar a medir, y una serie de elementos que nos permitan determinar un punto dentro del espacio. En el caso del espacio euclídeo se utilizan los denominados ejes. Un eje es una recta con una dirección determinada sobre la cual podemos medir.
En el caso concreto de 2D se usa el siguiente origen y ejes:

En este dibujo O es el origen desde el que se empieza a medir y X e Y son los ejes sobre los que se miden. Para determinar un punto P dentro de un espacio de 2D se necesitan dos números o coordenadas (uno en el eje X y otro en el eje Y).

Esta es la forma matemática que se enseña en las escuelas, pero no es la forma que se utiliza en la programación de videojuegos. En videojuegos el origen de coordenadas es la esquina superior izquierda de la pantalla. Y las coordenadas Y se incrementa hacia abajo.

nota:
La razón de que sea este sistema de coordenadas es por la forma que tenían las televisiones y monitores de rayos catódicos de formar la imagen que se hacia moviendo un haz de luz desde la esquina superior izquierda hasta la esquina inferior derecha realizando un barrido de izquierda a derecha y de arriba a abajo.

En SFML 2.0 se utiliza la clase sf::Vector2 en sus variantes punto flotante, entero y entero sin signo para representar un punto en el espacio 2D. (También existe el sf::Vector3 para espacio 3D, pero no nos interesa en este momento).

¿Dónde estas? ¿A qué distancia? Los Vectores

En física y en matemáticas a menudo es necesario representar algo mas que los puntos que determinan una posición en el espacio euclídeo, también es necesario representar de forma matemática (entendible por el ordenador) hacia donde se mueven los objetos y que distancia recorren. Por ejemplo: La velocidad de una nave tiene por una parte una dirección ( hacia el norte ) y por otra una magnitud ( los metros por segundo que recorre ).

Para representar esas múltiples características se utilizan los denominados Vectores. Un vector tiene tres características:

Tiene una dirección
Tiene un sentido
Tiene una magnitud

En este dibujo la línea gris (QP) es un vector, tiene una dirección, la línea que pasa por los puntos P y Q, tiene un sentido, se mueve desde el punto Q al punto P (la flecha indica el sentido ) y tiene una magnitud, la distancia desde Q hasta P.

Otro vector seria la línea roja que va desde el origen O hasta el punto Q. Es decir que todos los puntos pueden considerarse vectores con origen el centro de coordenadas, dirección la línea que para por el centro O y por el punto Q, sentido desde O hacia Q y magnitud la distancia de O a Q.

Así matemáticamente se puede representar un punto con dos números (coordenadas) y ese punto es a su vez un vector. Así pues se puede representar un vector con dos coordenadas. Es decir, matemáticamente un punto y un vector se representa igual, pero tienen interpretaciones diferentes.
En la practica, como programadores, nos da lo mismo un punto que un vector y por eso ambos se pueden representar con la clase sf::Vector2.

La importancia de Pitágoras. Longitud de los Vectores.

Si somos un poco espabilados, podemos darnos cuenta que un vector y un triangulo rectángulo están estrechamente relacionados.

El vector OP forma dos triángulos rectángulos. El formado por OPA donde A es el punto sobre el eje X que proyecta P. El otro es el OPB donde B es el punto sobre el eje Y que proyecta P.
Usando el teorema de Pitágoras podemos fácilmente calcular la distancia o longitud del vector OP.

OP² = OA² + AP²

Queremos haya OP. Conocemos OA, que es la proyección de P sobre el eje X, y que se corresponde con la coordenada X del punto P: Xp. Por el otro lado AP es igual a OB que es la proyección del punto P sobre el eje Y, es decir, la coordenada Y del punto P: Yp.

OP² = Xp² + Yp²

Despejando obtenemos:

$_LARGE_!OP=_sqrt{XP^2 YP^2}$

Con esto ya sabemos como calcular la longitud de un vector. Esta operación no está incluida como parte de la clase sf::Vector2, pero le haremos un añadido más adelante.

Operando con vectores

Como con cualquier objeto matemático se han definido una serie de operaciones para manipular los vectores. Aquí tenemos las operaciones básicas de suma, resta y multiplicación por un escalar (se denomina escalar a un numero simple, es oposición con un vector que es la composición de 2 o mas coordenadas ).

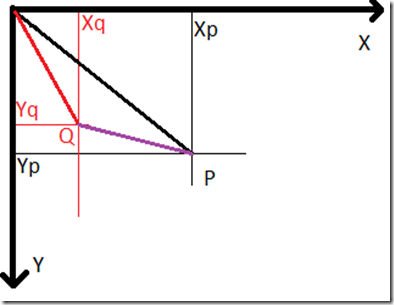
La suma de dos vectores da como resultado otro vector. Visualmente se puede decir que para sumar dos vectores se coge uno de ellos y se mueve su origen hasta el punto final del otro. Esto nos dibuja la siguiente situación. El vector violeta OR es la suma de los vectores OP y OQ

OR = OP + OQ

Si nos fijamos la proyección de OQ es x es Xq. Si movemos el origen de OQ hasta el final del vector OP, es decir, movemos la longitud en x Xq hasta el punto P obtenemos la proyección en x del vector OR que es:

Xr = Xp + Xq

Y de la misma forma en el eje Y:

Yr = Yp + Xq

La conclusión es que el vector suma de dos vectores es igual al vector resultante de la suma de las componentes.

OR = OP + OQ = [Xp,Yp] + [Xq,Yq] = [ (Xp+Xq) , (Yp+Yq) ] = [Xr, Yr]

Una de las propiedades de la suma de vectores es que OP + OQ es igual que si hacemos OQ + OP.

La resta de dos vectores también da otro vector.

Visualmente, la resta es el vector que se forma desde el final de un vector hasta el final del otro. En este caso:

OP – OQ = PQ

Se podría interpretar como la suma de un vector con el otro vector multiplicadas sus componentes por –1.

PQ = OP + (-1 * OQ) = [Xp, Yp] + [ (-1*Xq), (-1*Yq)] = [Xp + (-Xq), Yp + (-Yq)] = [ Xp-Xq,Yp-Yq]

Así que la resta es un vector cuyas componentes es la resta de las componentes de los vectores que se restan.

A diferencia de la suma OP – OQ = PQ no es lo mismo que OQ – OP = QP, ya que el sentido del nuevo vector son diferentes. Un vector que parte de Q para llegar a P se calcula como OP – OQ, mientras que un vector que parte de P para llegar a Q se calcula como OQ – OP.

La multiplicación por un escalar obtiene un vector que tiene la misma dirección, el mismo sentido, pero con una longitud multiplicada por el escalar.

k * OP = k*[Xp, Yp] = [k*Xp, k*Yp]

La división entre un escalar es igual.

NOTA

Existe un vector denominado vector unitario o vector director que es aquel vector que tiene una longitud igual a uno. Es especial por que tiene la dirección y sentido de un movimiento. Multiplicando lo por el valor escalar de la velocidad, por ejemplo, se obtiene el vector velocidad.

Para calcular el vector director solo hay que dividir un vector entre su longitud para obtener longitud uno. Esta operación de obtener es vector director tampoco esta en sf::Vector2 y la añadiremos.

Las rarezas de los vectores: Producto Escalar y Vectorial

Estas dos operaciones son exclusivas de los vectores.
El primero es el productor escalar o producto punto (dot product en ingles). El resultado es un numero (un escalar) cuya interpretación es la multiplicación de las longitudes de los vectores por el coseno del Angulo que forman.

Es decir que:

OP · OQ = |OP| * |OQ| * cos( a )

Siendo |OP| y |OQ| las longitudes de los vectores OP y OQ respectivamente.

Esta operación resulta muy útil para saber a que lado están las cosas. Si tomamos que el vector rojo A es el vector hacia donde estamos mirando, el signo del producto escalar nos permitirá saber si un objeto esta delante o detrás de nosotros.

Si el vector violeta B es el vector desde mi posición hasta la posición de un objeto, calculando el producto escalar de los vectores, el signo de la operación saldrá positivo, pues la proyección del vector B sobre el vector A esta en el mismo sentido, indicando que esta delante de mi.

Si el vector azul D es otro vector desde mi posición a otro objeto, el calculo del producto escalar será negativo pues la proyección del vector D sobre el vector A tienen sentidos distintos.
Por otro lado, Si proyectamos el vector naranja C sobre el vector A, vemos que es cero, es decir el producto escalar de dos vectores perpendiculares ( que forman 90º ) es cero.

NOTA
Con esta operación podemos saber si un personaje esta delante o detrás de una pared. Si una pelota esta delante o detrás de un jugador, etc.…

Para calcular el producto escalar de dos vectores OP y OQ se realiza el siguiente calculo:

OP · OQ = [Xp,Yp] · [Xq,Yq] = Xp*Xq + Yp*Yq

nota:

Como curiosidad, y para que si lo veis por hay no os extrañéis. El productor escalar de un vector consigo mismo es igual al cuadrado de la longitud del vector.

Veámoslo:

OP · OP = [Xp,Yp] · [Xp,Yp] = Xp*Xp + Yp*Yp = Xp² + Yp²

Así que a veces podéis encontrar que para calcular la distancia entre dos puntos se calcula el productor escalar entre los vectores que definen los puntos.

El productor vectorial por otro lado es una operación de la que se obtiene otro vector, pero es nuestro estudio carece de utilidad, pues el vector obtenido es perpendicular a los dos vectores multiplicados. Es decir estarán sobre un eje Z que saldría desde la pantalla del ordenador.

Trigonometría: Relación entre triángulos y ángulos

Toda la trigonometría se basa en la relación que existe entre un triangulo rectángulo y los ángulos que forman sus lados.

Para estudiar la trigonometría se utiliza como referencia visual una circunferencia de radio unidad sobre la que un radio con cierto ángulo proyectado sobre los ejes de coordenadas forma un triangulo rectángulo.

Así el radio que forma un ángulo a con el eje X (origen de los ángulos), al proyectarse sobre los ejes de coordenadas forma un triangulo rectángulo ABC. A partir de este triangulo se definen las funciones matemáticas:

Coseno: Se define como la división entre el lado opuesto al ángulo entre la hipotenusa del triangulo:

cos(a) = |CB| / |AC|

Si tenemos en cuenta que |AC| es el radio de la circunferencia y esta tiene radio 1 entonces:

cos(a) = |CB|

Que es el lado representado de rojo.

Seno: Se define como la división entre el lado adyacente al ángulo entre la hipotenusa del triangulo:

sin(a) = |AB| / |AC|

Al igual que entes |AC| = 1 y el seno es entonces:

sin(a) = |AB|

Representado por el lado violeta del triangulo.

Tangente: Se define la división entre el lado adyacente al ángulo entre el lado opuesto al ángulo:

tan(a) = |AB| / |CB|

que si tenemos en cuenta los dos anteriores resulta:

tan(a) = sin(a) / cos(a)

Gráficamente se representa por la línea verde, que es la proyección desde el punto en que la circunferencia intersecta al eje x positivo sobre la línea que define el ángulo.

Teniendo en cuenta que estamos hablando de los lados de un triangulo rectángulo podemos aplicar el teorema de Pitágoras:

|AC|² = |AB|² + |BC|²

Teniendo en cuenta las funciones trigonométricas, resulta que:

|AC|² = sin(a)² + cos(a)²

Además, como |AC| es el radio de la circunferencia y este es uno resulta que:

1 = sin(a)² + cos(a)²

Existen también las funciones inversas que permiten hallar un ángulo a partir de su seno (arco seno), coseno (arco coseno) o de la tangente (arco tangente).

El más útil es el arco tangente, pues con el podemos hallar el ángulo de un vector a partir de sus componentes.

Si tenemos un vector OP el ángulo que forma con el eje X es a. Sabemos que la tangente de a es:

tan(a) = sin(a) / cos(a) = Yp / Xp

Con lo cual sabemos el valor de la tangente dividiendo la componente Y entre la componente X.

Si usamos la función matemática arco tangente, podemos hallar el ángulo que forma OP con X:

a = atan( tan( a ) ) = atan( Yp / Xp )

Aunque la función atan existe y se puede utilizar en C, es mejor usar otra función de la librería estándar de C, la función atan2 que recibe dos parámetros, el primero es la componente Y y el segundo es la componente en X. Esta segunda función nos devuelve no solo el Angulo entre 0 – 180 sino también el signo del giro, cosa que la función atan no lo hace.

NOTA
Las funciones matemáticas de la librería estándar de C funciona con ángulos en radianes.
Una circunferencia, que 360º, tiene 2 * PI radianes, siendo PI = 3.14159…, así para transformar un Angulo sexagesimal a un Angulo en radianes hay que utilizas la relación: