Colisiones y el maravilloso mundo de las matemáticas
Como deberíais saber lo que vemos en pantalla solo es una representación visual de una descripción matemática de un mundo, es decir que en realidad la nave ni existe ni es solida, por lo que nunca chocara con nada. Para que los objetos parezcan que chocan entre si necesitamos hacer los cálculos matemáticos necesarios para, según la posición y forma de los objetos, saber si en un determinado momento estos se solapan ( colisionan ).
En nuestro maravilloso mundo del Asteroid, las colisiones se relazan entre las balas y las rocas, haciendo que estas ultimas se fragmenten hasta que son pequeñas, que entonces se eliminan y entre las rocas y la nave, de forma que si choca con la nave se quita una vida al jugador y se vuelve a empezar.
Por como representamos los distintos elementos tenemos dos tipos de solapamiento que calcular:
- Circulo – Punto: Las rocas son círculos, mientras que las balas son puntos, así que habrá que averiguar si alguna bala esta dentro del radio de una roca.
- Circulo – Triangulo: Las rocas son círculos y la nave es un triangulo, habrá que averiguar si los segmentos que forman el triangulo están dentro de alguna de las rocas.
Preliminares: Añadiendo algunos métodos útiles.
Lo primero que vamos a hacer es añadir unos cuantos métodos a nuestras clases que nos ayudaran con posterioridad a calcular las colisiones.
En nuestra clase Ship vamos a añadir un método que nos permita saber cual es la posición en pantalla de los tres puntos que formal el triangulo de la nave:
En ship.h añadimos un método publico:
//B- Obtener los tres puntos de la nave void getPoints( sf::Vector2f& point_a, sf::Vector2f& point_b, sf::Vector2f& point_c );
Como veréis le pasamos tres sf::Vector2f como referencia, es decir, podemos modificar desde el método los valores de las variables externas a la clase.
En ship.cpp desarrollaremos el método:
//B- Obtener los tres puntos de la nave
void Ship::getPoints( sf::Vector2f& point_a, sf::Vector2f& point_b, sf::Vector2f& point_c )
{
point_a = getTransform().transformPoint( sf::Vector2f( 10.0f, 0.0f ) );
point_b = getTransform().transformPoint( sf::Vector2f(-10.0f, 7.5f ) );
point_c = getTransform().transformPoint( sf::Vector2f(-10.0f,-7.5f ) );
}
La nave tendrá una posición y giro determinada por el jugador, esta transformación esta registrada matemáticamente en la clase base sf::Transformable y se puede obtener por el método getTransform(). Usaremos esta transformación para obtener cual es la posición en pantalla de los puntos que forman el triangulo. Si observáis los puntos que he utilizado son los mismos con los que cree el objeto sf::ConvexShape que usamos para dibujar la nave.
En nuestra clase Bullet necesitaremos un método que nos permita “matar” la bala si choca con una roca, ya que no queremos que siga usándose después de chocar. La bala hasta ahora solo se moría de “vieja”.
En Bullet.h añadimos como método publico:
//A - Mata esta bala void kill();
En Bullet.cpp añadimos la definición del método:
void Bullet::kill()
{
m_is_alive = false;
}
Como veis es una tontería, simplemente marcamos m_is_alive como falso y nuestro código se encargara de eliminar la bala en la próxima actualización.
En nuestra clase Rock vamos a añadir unos métodos que nos ayuden a cambiar su tamaño y dirección, y a saber de que nivel es el objeto.
En Rock.h vamos a añadir tres nuevos métodos públicos:
//A - Coger el nivel de esta roca sf::Uint8 getRockLevel(); //A - Aumenta el nivel de la roca haciendolo mas pequeño void incrementRockLevel(); //A - Cambiar el Angulo de movimiento void changeMovementAngle(float new_movement_angle);
Un método para averiguar el nivel de la roca (0 – grande, 1 – mediano, 2 – pequeño ). Otro método se encargara de incrementar el nivel de la roca, hacerla mas pequeña, y un tercer método nos permitirá cambiar la dirección del movimiento. Esto nos vendrá bien cuando la roca colisione con una bala.
En Rock.cpp añadimos las definiciones de los métodos.
//A - Coger el nivel de esta roca
sf::Uint8 Rock::getRockLevel()
{
return m_rock_level;
}
//A - Aumenta el nivel de la roca haciendolo mas pequeño
void Rock::incrementRockLevel()
{
++m_rock_level;
if( m_rock_level > 2 )
{
m_is_alive = false;
return;
}
m_rockShape.setRadius( rock_radius[ m_rock_level ] );
m_rockShape.setOrigin( rock_radius[ m_rock_level ], rock_radius[ m_rock_level ] );
}
//A - Cambiar el Angulo de movimiento
void Rock::changeMovementAngle(float new_movement_angle)
{
m_direction_of_movement = sf::Vector2f( std::cosf( new_movement_angle * degree2radian), std::sinf( new_movement_angle * degree2radian ) );
}
El método getRockLevel simplemente devuelve la variable miembro m_rock_level. El método incremetRockLevel aumentara el valor de m_rock_level, si este es mayor que el máximo, “matara” esta roca, si no adaptara el objeto sf::CircleShape que representa esta roca según el radio que corresponde al nuevo nivel. el método changeMovementAngle recibe un nuevo Angulo (en grados) y calcula el nuevo vector de movimiento.
Colisión Circulo – Punto
Nuestras rocas están definidas por un punto, el centro de la circunferencia, y un radio en función de su nivel. Teniendo en cuenta esto, un punto cuya distancia al centro de la roca sea mayor que el radio de la roca estará fuera de la roca y por lo tanto no chocaran. Por el contrario si la distancia entre el punto y el centro de la roca es menor que el radio significa que han colisionado.

NOTA:
La distancia entre dos puntos se define como la longitud del vector que une los dos puntos.
El vector entre dos puntos se define como la resta de los componentes de los puntos. Dado el punto A[ax,ay] y el punto B[bx,by] el vector que va desde A hasta B es: AB [ (bx – ax), (by – ay) ]
La longitud de un vector se define como la raíz cuadrada de la suma de los cuadrados de las componentes. la longitud del vector AB es |AB| = Sqrt( (bx – ax) * (bx – ax) + (by – ay)*(by – ay) ).
En videojuegos tradicionalmente se suele usar las distancias al cuadrado para evitar tener que calcular la raíz cuadrada que es una operación matemática muy costosa en ciclos de computación y que si se tuviera que hacer cientos o miles de veces, haría perder algunos frames al juego.
En nuestra clase Rock vamos a introducir un nuevo método que nos diga si un punto esta colisionando con la roca o no.
En Rock.h introducimos un nuevo método publico:
//A - Check the collision with a point bool checkPoint( const sf::Vector2f& point );
Le pasamos un punto en forma de vector que será la posición de la bala.
En Rock.cpp implementamos la definición:
//A - comprueba la colision con un punto
//Se hallara la distancia desde point hasta el centro
//si es menor que el radio es que colisionan
bool Rock::checkPoint( const sf::Vector2f& point )
{
float cx = getPosition().x;
float cy = getPosition().y;
float x0 = point.x;
float y0 = point.y;
//Distancia al punto
float SqrDist = (( cx - x0 ) * ( cx - x0 )) + (( cy - y0 ) * ( cy - y0 ));
float SqrRadius = rock_radius[ m_rock_level ] * rock_radius[ m_rock_level ];
return (SqrDist <= SqrRadius);
}
Como podéis observar, simplemente sigo los pasos para hallar la distancia al cuadrado entre el punto y el centro (posición de la roca) y la comparo con el radio al cuadrado, si es menor o igual es que el punto esta dentro o justo en el circulo y devolverá un cierto.
Colision Circulo – Triangulo
Este tipo de colision es un poco mas complejo matemáticamente hablando ya que requiere de algunos conocimientos avanzados de geometría.
Primero hay que decir que un triangulo puede asimilarse a tres segmentos que comparte puntos en común. Por lo tanto descompondremos la colision entre la nave y la roca como la colision de la roca y tres segmentos.
Un segmento se define como un trozo de recta. Por lo tanto la intersección entre un circulo y un segmento es solo un caso particular de la intersección de una circunferencia y una recta.
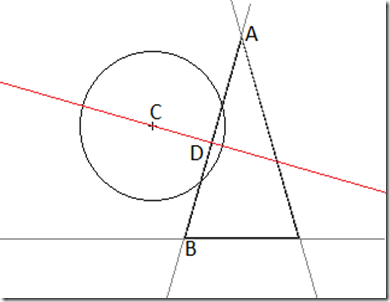
Nuestro problemas es que queremos hallar el punto D del dibujo de arriba. Este punto es la mínima distancia entre el centro de la circunferencia y la recta AB.
Sabemos que la recta que pasa por A y B tiene la misma dirección que el vector AB.
Sabemos que la recta que pasa por C y por D forma un Angulo de 90º con respecto a la recta AB, por lo tanto sabemos cual es la dirección del vector CD pues forma 90º con el vector AB.
NOTA:
Dado un vector A(x,y), un vector ortogonal ( con la dirección 90º) con respecto a este será un vector con las componentes cambiadas y una cambiada de signo, es decir, B( -y,x),
Sabemos que el punto D pertenece a la recta AB y también pertenece a la recta CD, por lo tanto la ecuación de la recta AB será igual a la ecuación de la recta CD en esas coordenadas.
NOTA:
Una recta puede definirse por una ecuación basada en un punto y una pendiente (Angulo entre la recta y el eje de coordenadas x)
Resolviendo la igualdad de las ecuaciones en el punto D, hallaremos las coordenadas del punto.
Se dice que el segmento y la circunferencia se solapan (colisionan) cuando la distancia desde A hasta C o la distancia desde B hasta C es menor que el radio (si es así seguro que colisionan) o si la distancia desde C hasta D es menor que el radio (si fuera mayor se descartaría la colision) y el punto D esta entre el punto A y el punto B (es decir que si esta fuera del segmento no colisionarían).
Bueno, veamos el código. Primero en Rock.h añadimos dos métodos públicos:
//B - Check the collision with a triangle bool checkTriangle( const sf::Vector2f& point_a, const sf::Vector2f& point_b, const sf::Vector2f& point_c); //B - Check the collision with a segment bool checkSegment( const sf::Vector2f& point_a, const sf::Vector2f& point_b);
Simplemente en uno se proporcionan los puntos que forman el triangulo y en otro los puntos que forman un segmento.
Ahora a por la “chicha” en Rock.cpp.
//B - comprueba la colision con un triangulo
//hace una comprobación de los tres segmentos
bool Rock::checkTriangle( const sf::Vector2f& point_a, const sf::Vector2f& point_b, const sf::Vector2f& point_c )
{
bool a = checkSegment( point_a, point_b );
bool b = checkSegment( point_b, point_c );
bool c = checkSegment( point_c, point_a );
return (a || b || c );
}
//B - comprueba la colision con un segmento de línea
bool Rock::checkSegment( const sf::Vector2f& point_a, const sf::Vector2f& point_b )
{
//Para facilitar el código cogemos en x0, y0 el centro del circulo
float x0 = getPosition().x;
float y0 = getPosition().y;
//Calculamos el radio al cuadrado para luego
float SqrRadius = rock_radius[ m_rock_level ] * rock_radius[ m_rock_level ];
//Calculamos las distancias al cuadrado entre el centro del circulo y los puntos del segmento
float SqrDistA = (( point_a.x - x0 ) * ( point_a.x - x0 )) + (( point_a.y - y0 ) * ( point_a.y - y0 ));
float SqrDistB = (( point_b.x - x0 ) * ( point_b.x - x0 )) + (( point_b.y - y0 ) * ( point_b.y - y0 ));
//Si alguno es menor que el radio, se terminaron los cálculos están colisionando
if( SqrDistA <= SqrRadius ) return true; //El punto A esta dentro del circulo
if( SqrDistB <= SqrRadius ) return true; //El punto B esta dentro del circulo
//Se calcula el vector perpendicular al vector del segmento AB
float A1 = point_b.y - point_a.y;
float B1 = point_a.x - point_b.x;
//Se calcula las partes que forman la igualdad de las ecuaciones del
//segmento AB y del segmento XC con X centro de la circunferencia y
//C punto de intersección de las rectas
double C1 = (point_b.y - point_a.y)*point_a.x + (point_a.x - point_b.x)*point_a.y;
double C2 = -B1*x0 + A1*y0;
double det = A1*A1 - -B1*B1;
double cx = 0;
double cy = 0;
if(det != 0)
{
//Se resuelve la igualdad y se halla las coordinadas de la intersección
cx = (float)((A1*C1 - B1*C2)/det);
cy = (float)((A1*C2 - -B1*C1)/det);
}
else //Si det es cero significa que X == C
{
cx = x0;
cy = y0;
}
//Distancia del centro de la circunferencia y el punto de intersección
float SqrDistC = (( cx - x0 ) * ( cx - x0 )) + (( cy - y0 ) * ( cy - y0 ));
if( SqrDistC > SqrRadius ) return false; //Demasiado alejado para colisionar
//Se mira si el punto de intersección esta fuera del segmento en el eje X
if( cx < std::min<float>( point_a.x, point_b.x) ) return false; //Fuera del segmento por abajo en x
if( cx > std::max<float>( point_a.x, point_b.x) ) return false; //Fuera del segmento por arriba en x
//Se mira si el punto de intersección esta fuera del segmento en el eje Y
if( cy < std::min<float>( point_a.y, point_b.y) ) return false; //Fuera del segmento por abajo en y
if( cy > std::max<float>( point_a.y, point_b.y) ) return false; //Fuera del segmento por arriba en y
//Si se supera todos los tramites se dice que han colisionado
return true;
}
He puestos comentarios para entender a grandes rasgos que se esta haciendo. Como podéis comprobar se tratara siempre de realizar el menor numero de cálculos posibles, por eso hay tantos return en el código. Si una condición nos garantiza que colisiona (como que la distancia a uno de lo puntos desde el centro de la circunferencia sea menor que el radio) ya no se calcula mas.
Calculando las colisiones en el juego
Por ultimo vamos a realizar dentro de nuestro bucle principal de juego en main.cpp el calculo de las colisiones y las consecuencias de estas. El código se realizara justo al principio del bucle, aunque también se podría haber echo después del dibujado.
Veamos el código:
//A - comprobamos las colisiones de los asteroides y las balas
//Aquí almacenaremos las nuevas rocas que se generen por la colision roca-bala
std::vector<game::Rock*> addedRocks;
//Recorremos todas las rocas
RockIndex RI0 = rocks.begin();
RockIndex RE0 = rocks.end();
while( RI0 != RE0 )
{
game::Rock* rock = (*RI0);
//Recorremos todas las balas
BulletIndex I = bullets.begin();
BulletIndex E = bullets.end();
while( I != E )
{
game::Bullet* bullet = (*I);
//Si la bala no esta viva se pasa a la siguiente
if( !bullet->isAlive() )
{
++I;
continue;
}
//Comprobamos la colision
if( rock->checkPoint( bullet->getPosition() ) )
{
//Matamos la bala para evita que una misma bala destruya varias rocas
bullet->kill();
//recicla esta roca incrementando su nivel y cambiando si dirección
rock->incrementRockLevel();
rock->changeMovementAngle( std::rand()%360 );
//Si era una roca con nivel menor que 2 seguirá viva
//y habrá que añadir una nueva roca del mismo nivel
if( rock->isAlive() )
{
game::Rock* newRock = new game::Rock( sf::Vector2f( rock->getPosition().x, rock->getPosition().y ) , std::rand()%360, rock->getRockLevel() );
//No se añade directamente, sino que se almacena para añadirse al final
addedRocks.push_back( newRock );
}
//Si esta roca colisionado ya no se prueba mas y se para a la siguiente
break;
}
++I;
};
++RI0; //siguiente roca
};
rocks.insert( rocks.end(), addedRocks.begin(), addedRocks.end() );//insertar las rocas nuevas
//Cogemos los puntos en pantalla que representan a la nave
sf::Vector2f point_a, point_b, point_c;
space_ship.getPoints( point_a, point_b, point_c );
//Nueva mente recorremos todas las rocas
RI0 = rocks.begin();
RE0 = rocks.end();
while( RI0 != RE0 )
{
game::Rock* rock = (*RI0);
//Si colisiona necesitamos por el momento reiniciar el juego
//Mas adelante contaremos las vidas, los puntos y el "game over"
if( rock->checkTriangle( point_a, point_b, point_c ) )
{
need_reset_game = true;
break;
}
++RI0; //siguiente roca
};
En los comentarios encontrareis que se hace en cada fase del calculo de las colisiones.Por el momento cuando choquen la nave y las rocas simplemente reiniciaremos el juego, Si acabas con todas las rocas no pasara nada. La próxima entrada terminaremos el juego con los elementos que faltan, unas explosiones, contar los puntos y las vidas y subir de nivel cuando limpies una pantalla.
Una cosa importante es que no podéis añadir elementos a una lista mientras la estáis recorriendo, pues dejaría invalidas las variables de inicio y final que se usan para recorrerlos, es mejor almacenarlas en un vector y luego añadirlos todos en bloque al final.
Podeis descargar el código aqui
Gracias por vuestra atención.

1 comentario:
Muy interesante este blog.
La verdad, se agradecen mucho estos tutoriales de SFML :)
Publicar un comentario